Úvaha k interpretaci faktoru difúzního odporu kapilárně pórovitých materiálů
Doc. Ing. Jan Krňanský, CSc., katedra pozemního stavitelství FUA TU v Liberci
Autor děkuje za pomoc při zpracování příspěvku Ing. Ivanu Misarovi ze společnosti A.W.A.L. s.r.o.
1. Materiálově-inženýrský přístup
V poslední době vzniká v inženýrské praxi potřeba aktivně navrhovat nejen stavební konstrukce, ale i samotné výchozí materiály, z nichž se tyto konstrukce tvoří. Příkladem mohou být tzv. difúzně otevřené konstrukce, kde je třeba zajistit specifické transportní vlastnosti. „Konstruování“ materiálů s určitými požadovanými vlastnostmi spadá do oblasti rychle se rozvíjejícího oboru, materiálového inženýrství.
Základním východiskem pro inženýrskou činnost v oblasti materiálů je pochopení procesů, které ve hmotách resp. v jejich pórových systémech skutečně probíhají. Tato úvaha je věnována interpretaci jedné z důležitých charakteristik molekulárního přenosu plynů a par v pórových systémech stavebních hmot, faktoru difúzního odporu.
2. Fenomenologická interpretace faktoru difúzního odporu
Ve stavební fyzice obvykle pojímáme vlhký vzduch jako binární směs, mající za složky suchý vzduch a vodní páru. Jako výchozí přenosovou (fenomenologickou) rovnici pro výpočet hustoty difúzního toku složek se zavádí výraz
![]()
kde D je součinitel vzájemné difúze obou složek směsi, ci je příslušná koncentrace složky (viz dále). Uvažujeme tedy pouze tzv. koncentrační difúzi, kdy je hnací silou difúze gradient molární nebo hmotové koncentrace složek.
 obr. 1: Za konstantního celkového tlaku a teploty probíhá tzv. ekvimolární difúze, kdy počet difundujících částic (molekul)obou složek je přesně stejný.
obr. 1: Za konstantního celkového tlaku a teploty probíhá tzv. ekvimolární difúze, kdy počet difundujících částic (molekul)obou složek je přesně stejný.
Uvedený vztah pro koncentrační difúzi není obecný; v případě proměnné molární resp. hmotové hustotě směsi jako celku bychom měli pracovat s gradientem molárního resp. hmotového zlomku. Tato skutečnost se ve stavební fyzice (vesměs oprávněně) zanedbává.
Jako výchozí přenosovou rovnici pro výpočet hustoty difúzního toku složek pórovitým materiálem se analogicky zavádí výraz
![]()
rov. 2
kde μ je tzv. faktor difúzního odporu materiálu.
Základní technickou charakteristikou samotných materiálů pro výpočet difúzního přenosu v konstrukcích je tedy podle současné normové metodiky právě faktor difúzního odporu. Tato veličina je relativní hodnotou a stanovuje se jako podíl hustoty difúzního toku vodní páry suchým vzduchem k hustotě difúzního toku vodní páry rovněž suchým vzduchem, avšak v pórovém systému stavebního materiálu (za jinak stejných podmínek).
Tradiční strukturní interpretace faktoru difúzního odporu
Přibližme nyní obvyklou interpretaci této veličiny. V některých obecných úvahách je někdy názornější i přirozenější pracovat rovněž s veličinou k faktoru difúzního odporu reciprokou, s tzv. relativní difúzní prostupností neboli relativní difúzní permeabilitou.
1) Struktura přenosové rovnice
Přenosová rovnice tvrdí, že difúze pórovitým materiálem je vlastně difúze plynným prostředím (v případě stavební fyziky difúze vodní páry suchým vzduchem). Ke skutečnosti, že difúze „navíc“ probíhá pórovým prostředím stavebního materiálu, přihlédneme součinitelem μ. Implicitně tedy předpokládáme, že difúze je tzv. Fickovou difúzí, kdy molekulární tok vzniká v důsledku různých parciálních koncentrací složek směsi (podle způsobu popisu hmotnostních nebo molárních). Fickova difúze je ovšem makroskopickým projevem přenosu, uskutečňovaného výhradně vzájemnými srážkami molekul obou složek binární směsi.
2) vliv pórovitosti π
Intuitivně se zdá, že s rostoucí pórovitostí automaticky roste obecně i prostupnost materiálu pro plyny. Pokud se jedná o hutné materiály s jemnými pórovými systémy, můžeme vesměs zanedbat konvektivní složku přenosu. Jediným mechanismem je potom molekulární přenos (tj. „čistá“ difúze). Při diskusi o vlivu pórovitosti můžeme uvažovat ovšem pouze tzv. otevřenou pórovitost, tj. objem pórů, které jsou mechanismu difúze přístupné a vzájemně propojené. Do této pórovitosti tedy nemůžeme zahrnout objem uzavřených pórů a „kapes“. Ve stavební praxi je ovšem jen minimum materiálů, které mají pro difúzi skutečně uzavřené póry. S ohledem na velikost molekuly vody (průměr asi 3,1.10-10m) snadno ověříme, že prakticky všechny běžné stavební materiály s výjimkou kompaktů mají pórovitost, kterou můžeme chápat jako otevřenou.
Běžně se předpokládá, že propustnost pro difúzi je přímo úměrná ploše pórů na řezu materiálem. U převážné většiny stavebních materiálů platí stereometrický zákon, nazývaný také Delesse-Rosiwalův vztah. Ten tvrdí, že plocha pórů k celkové ploše rovinného řezu (tzv. plošná pórovitost πΣ ) je rovna pórovitosti objemové, πΣ= πv. Také o tuto zkušenost opíráme tvrzení, že propustnost pro difúzi je přímo úměrná pórovitosti.
3) Vliv zakřivení pórů (tortuozity) κ
Nechť je v tělese dán směr x, v němž probíhá difúze. Zvolme dvě roviny s pořadnicemi xA, xB, kolmé ke směru difúze. Vzdálenost bodů A, B je zřejmě Δx = xB – xA. Vyberme nyní elementární objem dV difundující složky (v termínech fyziky kontinua „materiálový bod“, viz např. /3/) a sledujme jeho pohyb z pozice A. Vlivem přítomnosti pevné fáze se elementární objem dV nemůže pohybovat přímočaře, pórový systém jej bude od přímé spojnice bodů A, B odklánět. Proto v okamžiku, kdy dosáhne rovinu s pořadnici xB, urazí dráhu Δs>Δx. Uražená dráha Δs se někdy nazývá proudové vlákno. Pokud lze podíl Δs/Δx považovat s ohledem na materiálovou strukturu za konstantu (samozřejmě ve statistickém smyslu slova), nazýváme jej tortuositou ![]() (klikatostí) pórového systému
(klikatostí) pórového systému
![]()
rov. 3
Při difúzi směrem s bude hnací síla úměrná veličině
![]()
rov. 4
Na základě této úvahy považujeme za zdůvodnitelné předpokládat, že difúzní prostupnost materiálu je nepřímo úměrná tortuozitě.
Z uvedených skutečností vychází obvykle užívaná „strukturní“ interpretace faktoru difúzního odporu (reciproká hodnota relativní difúzní permeability) ve tvaru
![]()
rov. 5
Tato častá a oblíbená interpretace je sice příjemně názorná a jednoduchá, bohužel však až na vyjímky neodpovídá skutečným jevům, probíhajícím v mikrostruktuře.
Základní problémy klasické strukturní interpretace
jsou dva:
a) v pórových systémech převážné většiny stavebních materiálů nejsou splněné podmínky Fickovy difúze (významný podíl celkového počtu srážek molekul tvoří jejich srážky s povrchem pórového systému),
b) vedle difúze molekul prostorem pórového systému se uplatňují i jiné mechanismy přenosu. U kapilárně pórovitých těles jde zejména o tzv. povrchovou migraci (v literatuře rovněž 2D difúze, povrchová difúze). Tento mechanismus vůbec na pórovitosti nezávisí; ze stereometrického hlediska však souvisí určitým způsobem s obvodem pórů na ploše rovinného řezu a také s délkou dráhy, kterou musí 2D difúzní tok po povrchu pórového systému urazit.
Výše naznačená tradiční zjednodušená „strukturní“ interpretace faktoru difúzního odporu proto nemůže umožnit správně pochopit a vyložit známé měřené souvislosti, jako je např. změna μ s jemností pórů při stejné celkové pórovitosti, změna faktoru difúzního odporu s vlhkostí materiálu atd. A co je podstatné z pohledu materiálového inženýrství, především neumožňuje spolehlivě určit vliv změny strukturních parametrů na přenosové schopnosti materiálu.
Proto se v dalším pokusíme o věcně správnou strukturní interpretaci laboratorně měřené hodnoty faktoru difúzního odporu (v tomto textu pouze pro případ kapilárně pórovitých těles).
3. Mechanismy molekulárního přenosu vlhkosti v materiálech
Makroskopická interpretace parametrů mikrostruktury a jevů v ní probíhajících musí mít u reálných materiálů vždy charakter jisté pravděpodobnostní výpovědi. Je to dáno nepřebernou členitostí a rozmanitostí mikrostrukturních útvarů, které vytvářejí v prostoru více či méně pevný skelet a tím také jeho objemový stereometrický doplněk, pórový systém.
Difúze objemem pórového systému (3D difúze)
Při hodnocení pórových systémů velké části kapilárně pórovitých materiálů (např. některé typy betonů, malt, keramiky, hornin apod.) snadno ověříme, že v nich klasická Fickovská difúze probíhá jen zčásti, nebo dokonce vůbec. Vyplývá to z toho, že za běžných klimatických podmínek je střední volná dráha molekuly vody λ ve vzduchu rovna cca 10-7m. Podle známého Knudsenova kritéria lze považovat difúzi za Fickovskou, jestliže je charakteristický rozměr d pórového systému (ve smyslu příčného řezu) roven alespoň 100 násobku hodnoty λ, tedy přibližně d≥10-5m. Srovnáním této hodnoty s distribucí pórů podle charakteristického rozměru (běžně užívaná představa válcových pórů kruhového průřezu) zjistíme ihned značnou omezenost předpokladu o čisté Fickově difúzi.

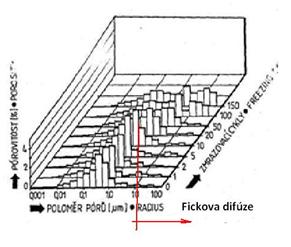
obr. 2: rozdělení pórů v cementové maltě za různých teplot (vlevo), zpracováno podle /5/, rozdělení pórů v pískovci při zmrazovacích cyklech (vpravo), zpracováno podle /6/.
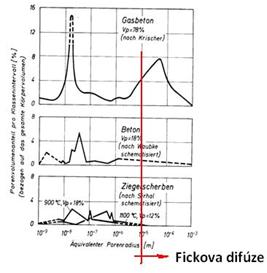
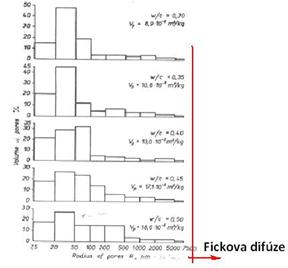
obr. 3: rozdělení pórů v různých kapilárně-pórovitých materiálech (vlevo), zpracováno podle /7/, a v cementové maltě podle různé hodnoty vodního součinitele, zpracováno podle /8/.
V menších pórech nastupují jak známo mechanismy jiné: pro efektivní rozměr pórového systému d≤10-8m nastává tzv. Knudsenova difúze, pro přechodovou oblast pórů (efektivní rozměr póru systému v rozmezí 10-8m ≤ d ≤ 10-5m) potom mechanismus, který je jistým hybridem difúze Fickovy a Knudsenovy (tzv. difúze v přechodové oblasti). Zajímavé ovšem je, že všechny tyto tři typy difúze je možné popsat jedním typem přenosové rovnice (viz např. /1/).
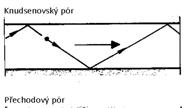
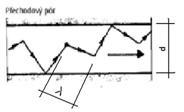

obr. 4: O zatřídění póru rozhoduje poměr střední volné dráhy molekuly λ k charakteristickému rozměru póru d. Ve všech schematech (průměry pórů nejsou zakresleny v poměru) předpokládáme stejnou střední volnou dráhu molekul, zpracováno podle /1/.
Faktor difúzního odporu se laboratorně nejčastěji zjišťuje metodou dry cup/wet cup. Měření probíhají za izotermních podmínek a za konstantního celkového tlaku směsi plynů (v našem případě směsi suchý vzduch-vodní pára). Vzniká tak ekvimolární difúze, tj. hustoty difúzních molárních toků vodní páry a suchého vzduchu jsou přesně stejně velké, opačného smyslu. Naměřenou hodnotu faktoru difúzního odporu, která je integrální interpretací většího počtu procesů, budeme nazývat efektivní hodnotou faktoru difúzního odporu, značíme μef. Přenosové rovnice pro jednotlivé velikosti pórů pak lze psát v jednotném tvaru (viz /1/)
![]() pro difúzi ve „Fickovských“ pórech, d≥10-5m
pro difúzi ve „Fickovských“ pórech, d≥10-5m
![]() pro difúzi v přechodových pórech, 10-8m ≤ d ≤ 10-5m
pro difúzi v přechodových pórech, 10-8m ≤ d ≤ 10-5m
![]() pro difúzi v Knudsenovských pórech, d≤10-8m
pro difúzi v Knudsenovských pórech, d≤10-8m
Ve vztazích je ci parciální molární koncentrace (mol/m3) příslušné složky binární směsi a Dxx (m2/s) jsou součinitelé vzájemné difúze pro každý dílčí typ přenosu. Pro součinitele Fickovské a Knudsenovy difúze vztahy
![]() kde D je součinitel vzájemné difúze suchého vzduchu a vodní páry,
kde D je součinitel vzájemné difúze suchého vzduchu a vodní páry,
![]() kde M je molární hmotnost difundující látky, T termodynamická teplota, d je charakteristický rozměr póru,
kde M je molární hmotnost difundující látky, T termodynamická teplota, d je charakteristický rozměr póru,
Pro určení součinitele difúze v pórech přechodového charakteru vyjděme z nejjednodušší představy, kdy požadujeme, aby hustota toku pórem byla lineárně závislá na efektivním rozměru na hranicích intervalu své platnosti (10-8m ≤ d ≤ 10-5m) byla rovna Knudsenovskému resp. Fickovskému difúznímu toku. Lze zřejmě psát
![]()
rov. 8
Poslední vztah je tedy lineární interpolace hustoty toku v oblasti mezi Knudsenovskou a Fickovskou difúzí a má tvar dobře známý v teorii interpolace (bázové funkce) v MKP.
Dosazením za ![]() a
a ![]() z rov. 6 máme vztah pro hustotu toku v přechodové oblasti
z rov. 6 máme vztah pro hustotu toku v přechodové oblasti
![]()
rov. 9
odkud ihned plyne pro součinitel difúze v přechodové oblasti (jako funkce poloměru póru)
![]()
Poslední vztah se přidružuje k rov. 7, čímž dostáváme úplnou sadu přenosových rovnic pro kapilárně pórové struktury. V přechodových pórech vždy nastane hustota toku menší než Fickovská. Je to logický důsledek narůstajícího počtu srážek molekul plynů se stěnami pórů při zmenšujícím se efektivním rozměru pórů.
Povrchová difúze (2D difúze, povrchová migrace)
Dalším typem přenosu, který automaticky měříme při laboratorním zjišťování hodnoty μef , je 2D difúze (povrchová difúze, povrchová migrace). Tento mechanismus, který se rozhodující měrou uplatňuje zejména ve velmi jemně pórovitých materiálech (zcela rozhodující je např. u zeolitů či nanotextilií), obecně na gradientu parciální molární koncentrace přímo nezávisí. Navíc se ukazuje, že vliv 2D difúze je podstatný i u materiálů s „nezeolitickou“ mikrostrukturou (viz dále).
Transmise
Konečně, není možné opomenout některé specifické transportní mechanizmy, které se často vyskytují u určitých skupin materiálů. Typickým příkladem je transmise molekul buněčnou stěnou u materiálů organického původu (zejména dřevo) a dále transmise molekul vody makromolekulárními látkami. Oba uvedené typy transmise mají pro stavební praxi velký význam.
Laboratorně zjištěná hodnota faktoru difúzního odporu µef , používaná ve stavebně-fyzikálních výpočtech, tedy v sobě obecně implicitně zahrnuje všechny výše uvedené mechanismy (v různých proporcích podle konkrétního typu materiálu a jeho mikrostruktury). Častá interpretace µ jako podílu tortuosity a pórovitosti je pro účely materiálového výzkumu nepřípustně zjednodušená a snad s vyjímkou materiálů typu vláknitých minerálních izolací vede ke zkreslení představ o skutečně probíhajících procesech v pórových systémech stavebních hmot.
4. Povrchová difúze molekul
Tento mechanismus je také nazýván plošnou, povrchovou či 2D difúzí. Jeho princip je následující.
Adsorpce
Povrch pevné fáze je typický tím, že směrem do volného prostoru existují nevysycená silová pole. Vznikají jako důsledek nerovnovážného mechanického stavu povrchových atomů v krystalech pevné fáze, kdy nejsou vykompenzovány jejich přitažlivé síly elektrické povahy směrem do nitra materiálu. V důsledku toho dochází k zachycování molekul okolního plynu na povrchu pevné fáze, čímž se současně zcela nebo alespoň částečně kompenzují zmíněná silová pole.
 obr. 5: na povrchu pevné fáze (levý okraj obrázku) dochází vlivem nevysycených povrchových sil k fyzikální adsorpci molekul, převzato z /9/.
obr. 5: na povrchu pevné fáze (levý okraj obrázku) dochází vlivem nevysycených povrchových sil k fyzikální adsorpci molekul, převzato z /9/.
Dochází-li k průniku elektronových obalů adsorbovaných molekul a pevné fáze, vzniká tzv. chemisorpce (chemická vazba, vazebná energie cca 80-800 kJ/mol). Tento jev potřebuje vysokou aktivační energii a za běžných teplot stavební praxe k němu téměř nedochází. Daleko častějším jevem je tzv. fyzikální adsorpce, zkráceně jen adsorpce (vazebná energie cca 0,1-10 kJ/mol). Adsorbované molekuly mají pouze dva stupně volnosti v tečné rovině povrchu pevné fáze. Vytvářejí tak dvourozměrný plyn (viz např. /2/, /4/), tj. systém molekul, které intenzivně migrují ve zmíněné tečné rovině povrchu. Je opět možné hovořit o hustotě 2D plynu, počtu srážek ve 2D plynu, střední volné dráze 2D plynu, 2D kondenzaci atd. Molekuly přímo na povrchu pevné fáze jsou ovšem vázány většími silami, než molekuly více vzdálené (v pomyslné druhé, třetí atd. vrstvě).
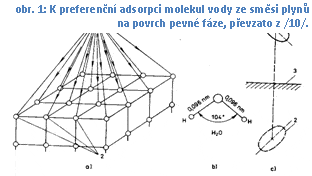
Preferenční adsorpce molekul vody
Jakmile začne probíhat difúze vodní páry do nitra materiálu, začne vznikat na vnitřním povrchu pórového systému adsorbovaný film molekul vodní páry. Tento jev ovšem není automatický. Je třeba uvážit, že vlhký vzduch je směsí celé řady molekul různých chemických látek. Molekula vodní páry tvoří ovšem dipól, který má ve světě molekul velký dipólový moment (v porovnání s ostatními molekulami, tvořícími suchý vzduch, je zdaleka největší, viz např. /2/). Proto vykazuje k povrchu pevné fáze daleko vyšší afinitu a dochází tak ze směsi plynů k preferenční adsorpci právě molekul vody.
 | |||
| |||

Povrchová migrace (2D difúze)
Nechť v čase t=0 dorazí na (vnější) povrch suchého materiálu „čelo“ vlny vodní páry. V tom okamžiku vzniknou dva jevy:
· začne probíhat 3D koncentrační difúze (libovolného typu) v pórovém systému materiálu, tedy pára proniká do nitra materiálu objemově, objemem pórů,
· na externím povrchu materiálu proběhne adsorpce molekul vody a vytvoří se 2D plyn chaoticky migrujících molekul. Tyto chaoticky migrující molekuly však začnou být okamžitě vtahovány do nitra materiálu nevysycenými silovými poli vnitřního suchého povrchu. Vznikne 2D tok molekul po povrchu pórového systému, směřující „od vlhkého k suchému povrchu“. Tento jev je právě předmětná povrchová migrace (2D difúze).
Jak prostorová difúze, tak i povrchová 2D difúze probíhají určitou rychlostí. Tyto rychlosti se nemusejí shodovat. Pokud jsou kapiláry, štěrbiny v materiálu velmi tenké, může probíhat „zásobování“ povrchu suchého materiálu molekulami z prostoru pórového systému velmi pomalu. Rychlejší a výkonnější pak může být zásobování povrchu suchého materiálu molekulami vody z vnějšího povrchu tělesa, tj. samotnou 2D difúzí.
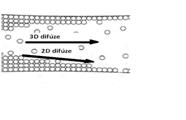
obr. 7: 2D difúze jako důsledek gradientu koncentrace 2D plynu na povrchu pevné fáze (pohyb „od vlhčího k suššímu“ povrchu). Směry 3D difúze a 2D difúze nemusejí být stejné.
Představme si nyní situaci v oblasti ústí velmi tenkého póru. Okolí ústí je pokryto vrstvičkou pohybujících se molekul 2D plynu. Povrchové síly pevné fáze naprosto nezávisejí na geometrii pórového systému. U velmi tenkých kapilár, štěrbin atd. se však vtahující účinky vlivem blízkosti protilehlých ploch zesilují. Logicky tedy zejména u velmi jemných kapilár (mikrotrhlin apod.) dochází k intenzivnímu vtahování molekul do nitra materiálu. 2D plyn difunduje po povrchu pevné fáze s konečným cílem rovnoměrně obsadit celý povrch pórového systému (termodynamická rovnováha fyzikálního systému). Intuitivně lze očekávat, že velmi jemně pórovité materiály (typicky silikagely a zeolity) mají velké potíže s objemovou difúzí, naopak však velmi efektivně využívají transport pomocí 2D difúze. Experimentálně je například u zeolitů (jemnozrnné jíly) ověřeno, že přenos vlhkosti 2D difúzí je několikanásobkem přenosu 3D difúze Knudsenovské (jiný typ 3D difúze ani nemůže v těchto materiálech nastat).
Kvalitativní souvislosti hustoty 2D difúzního toku
Existuje několik jednoznačných závislostí, určujících kvalitativně parametry 2D difúzního toku.
a. Elektrostatická povrchová aktivita materiálu: čím vyšší jsou povrchové elektrostatické přitažlivé síly dané materiálové báze, tím vyšší je i hustota 2D difúzního toku.
b. Měrný obvod pórů. Čím větší je obvod pórů na jednotkové ploše řezu, tím větší je zřejmě možný „nástupní prostor“ pro vnikání molekul mechanismem 2D difúze do nitra materiálu. Při dané pórovitosti budou zřejmě povrchově vodivější ty materiály, které mají jemnější póry. Měrný obvod pórů je svým významem jistým 2D analogem plošné pórovitosti.
c. Tortuozita povrchu. Vnitřní povrch materiálu je různě členitý. Pro ilustraci si představit přímou kapiláru mezi dvěma paralelními povrchy. Bude-li kapilára kolmá k povrchům, urazí molekula nejkratší dráhu. S rostoucím úhlem sklonu kapiláry bude (při stejné povrchové rychlosti) rychlost přenosu vzhledem ke kolmé kapiláře nutně klesat. Povrchová tortuozita je svým významem jistým 2D analogem obvyklé 3D tortuozity.
d. Teplota. Za izotermních podmínek bude mít 2D difúze směr od vlhčího k suššímu prostředí. Důvod je ten, že na vlhčí straně bude tloušťka adsorbované vrstvičky vyšší, než na straně suší. Vzniká tedy koncentrační gradient. Tato souvislost současně naznačuje, že pro sestavení fenomenologické rovnice bude možné využít rovnici difúzního typu.
Za neizotermních podmínek bude situace komplikovanější. Adsorbovaná molekula na povrchu pevné fáze podléhá trvalým silovým impulsům, které vyvolávají tepelné kmity krystalové mřížky, mj. i kolmo k povrchu krystalu (pevné fáze). Čím intenzivněji mřížka kmitá, tím hůře se adsorbovaná molekula na povrchu krystalu udrží. Amplituda kmitů s teplotou roste. Proto na teplejších površích bude za jinak stejné absolutní vlhkosti okolního vzduchu adsorbováno méně molekul, než na površích chladnějších. Hnací silou 2D difúze je i nadále gradient 2D koncentrace molekul. Směr 2D difúze však za neizotermních podmínek závisí na absolutních vlhkostech a teplotách vzduchu (potažmo materiálu) na přilehlých externích površích materiálu. Povrchové koncentrace vlhkosti, určující 2D difúzní tok, se určí z příslušných sorpčních izoterem.
Z uvedeného plyne, že povrchová migrace se bude výrazně uplatňovat zejména u jemně pórovitých materiálů, tj. u materiálů s vysokým měrným obvodem pórů. Výkonnost přenosu bude klesat s rostoucí povrchovou tortuozitou. Za izotermních podmínek bude směřovat z prostoru s vyšší relativní vlhkostí do prostoru s nižší relativní vlhkostí. Za neizotermních podmínek bude 2D difúze směřovat z míst s vyšším množstvím adsorbované vody do míst nižším množstvím adsorbované vody. Směřování lze určit z adsorpčních izoterem. Je tedy docela dobře možný (a běžný) 2D povrchový přenos z chladnějšího do teplejšího prostředí.
Intenzita 2D difúzního toku a mechanismus vypařování (ustálená 2D difúze)
Je velmi důležité si uvědomit, že 2D difúzní tok bezprostředně nesouvisí s tokem 3D difúze. Představme si pro jednoduchost přímou kapiláru jdoucí skrz stěnu, ustálený difúzní i teplotní stav. Všímejme si pouze jevu 2D difúze. Na vstupní straně je kapilára zásobována molekulami vodní páry ze vzduchu (adsorpce), po površích kapiláry ve stěně probíhá 2D difúze, na výstupní straně jsou molekuly vody odnímány mechanismem desorpce. Rychlost celého procesu tedy patrně souvisí s nejméně výkonným jedincem jmenovaného řetězce.
Adsorpce je výkonný mechanismus, který probíhá okamžitě (omezeno pouze rychlostí „dodávky“ molekul vodní páry z okolního vlhkého vzduchu na vstupní straně).
2D difúze povrchem póru je mechanizmus, který je zpravidla velmi účinný (vysoké povrchové energie suchého povrchu pórového systému).
Desorpce molekul na výstupní straně však již tak výkonná není. Jak známo, proces desorpce je stejně jako adsorpce neobyčejně rychlý, probíhá v podstatě okamžitě. Podmínkou ovšem je, aby prostředí na výstupní straně bylo připraveno desorbující se molekuly přijmout.
Poznámka: Jak je všeobecně známo z teorie vypařování, vytváří se nad hladinou kapaliny tenoučká vrstva syté páry. To, co určuje rychlost vypařování, není vypařování samo (dáno Maxwellovým rozložením rychlostí molekul v kapalině), ale rychlost, s jakou jsme schopni vypařující se kapalinu z vrstvičky syté páry odvádět. K odvodu syté vodní páry z tenké vrstvičky nad kapalinou mohou sloužit pouze dva mechanismy: difúze vodní páry do okolního vzduchu a dále proudění vzduchu nad povrchem kapaliny, tj. konvektivní odvod par.
(K výkonu čistého vypařování: kdybychom zajistili konstantní teplotu odpařující se kapaliny a dokázali odvést veškerou Maxwellovsky se vypařující kapalinu, činila by rychlost odparu 9 m vody za hodinu při 20°C. Skutečné odpařování v přírodě je 100 tis. až milión-krát pomalejší.)
U povrchového 2D vedení je situace analogická. Rychlost, intenzita 2D difúze je podmíněna výkonem výstupního mechanismu. 2D difúze bude pomalá, jestliže na výstupní straně bude nehybný vzduch (difúze par je pomalý proces). Za takových okolností bude hustota 2D toku odpovídat celkovému možnému difúznímu odvodu páry z povrchu do okolního prostředí (tok je dán součtem současně se desorbujících i 3D difundujících molekul do výstupního prostředí). Při existenci proudění, tj. při intenzivním odvodu desorbujících se molekul (současně s molekulami, opouštějícími materiál koncentrační difúzí) bude 2D přenos intenzivnější.
5. Kapilární kondenzace
V článku 4 identifikovaný mechanismus fyzikální adsorpce se jak známo nejlépe na makroskopické úrovni interpretuje pomocí sorpční izotermy. Při konstantní teplotě a celkovém tlaku prostředí zvyšujeme relativní vlhkost vzduchu. Na povrch materiálu se sorbuje stále více molekul, jejichž kvantitu vynášíme na svislou osu (hmotnost nebo látkové množství). Pro většinu kapilárně pórovitých stavebních materiálů má sorpční izoterma charakteristický S-tvar, obr. 8.
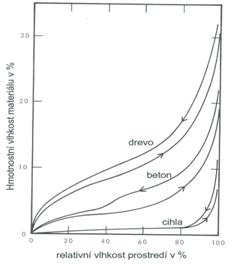
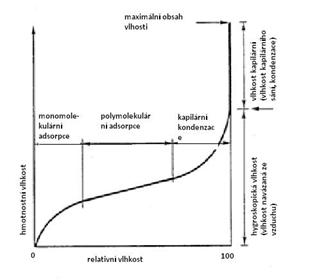
obr. 8: Sorpční izotermy některých stavebních materiálů (vlevo). Interpretace sorpční izotermy podle teorie multimolekulární adsorpce (teorie BET).
Podle známé interpretace pomocí teorie BET je první část izotermy odrazem monomolekulární adsorpce, střední část odrazem polymolekulární adsorpce a třetí, koncová část je odrazem kombinovaného jevu kapilární kondenzace+adsorpce. Tato část je charakteristická právě pro kapilárně-pórovité materiály, zatímco u jiných, například hrubě vláknitých struktur se prakticky nevyskytuje. Její interpretace má pro pochopení jevů v mikrostruktuře závažný význam.
Podstata kapilární kondenzace spočívá v tom, že při polymolekulární adsorpci v tenkých kapilárách resp. v zúženích běžných kapilár dojde při určité hodnotě relativní vlhkosti vzduchu (tj. při určité tloušťce polymolekulární vrstvy) ke značnému sblížení protilehlých povrchů adsorbovaných molekul. Mezi těmito povrchy začnou působit přitažlivé Van der Waalsovské síly a povrchy se skokovým procesem spojí, obr. 9.
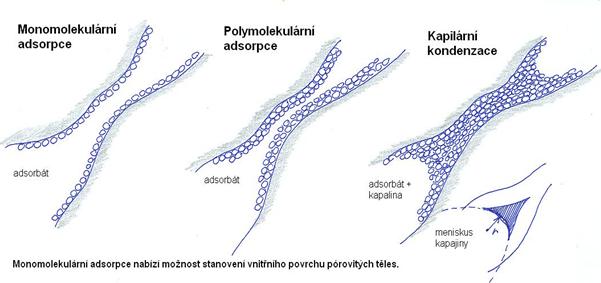
obr. 9: Mechanismus obsazování povrchu pórového systému, vznik kapilární kondenzace.
Zatímco adsorbovaná vrstvička vody má extrémní hustotu (pomocí TD úvah se odhaduje na 1500-1800 kg/m3), samotná voda kapilárně kondenzovaná již má vlastnosti normální vody. Je však ihned patrné, že jev kapilární kondenzace nemá nic společného s pojmem kondenzace, jak je užíván v běžném smyslu stavební fyzikou. U velmi jemných pórů se tento jev začíná uplatňovat již při nízkých hodnotách rh, cca od 20%.
Skokový jev spojení protilehlých povrchů kapilár má zásadní význam a vede ke změně kvality chování. Místa propojení povrchů vytvářejí „kondenzační jádra“, jisté body v pórovém systému, kde mohou začít fungovat fyzikální děje, spojené s přítomností kapalné fáze. Povrch kapilárně kondenzované vody v kapilárách vytvoří vysoce vyduté menisky (je-li povrch pevné fáze smáčivý vodou, což je velká většina kapilárně pórovitých stavebních materiálů). Vlivem většího počtu okolních molekul jsou potom molekuly na povrchu menisku vtahovány do kondenzátu silou větší, než na rovném povrchu. Proto z povrchu hladiny vyletuje (odpařuje se) menší počet molekul, než z rovné hladiny. Tenká vrstvička syté páry nad konkávním meniskem má tedy menší tenzi resp. molární koncentraci než pára nad rovnou hladinou. Zmíněnou závislost popisuje pro idealizovaný kruhový pór tzv. Kelvinova rovnice:
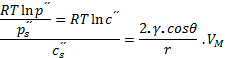
rov. 11
Kde index s značí rovný povrch, γ povrchové napětí vody, θ úhel smáčení, r poloměr menisku a konečně VM molární objem vody. p´´ je značka nasyceného tlaku par, c´´ pak nasycené molární koncentrace.
Horní hranice poloměru pórů, které lze identifikovat pomocí Kelvinovy rovnice, se udává asi hodnotou 300-500 Å, dolní hranice (kdy rovnice ztrácí fyzikální smysl), se udává poloměrem asi 18 Å. Znamená to, že kapilární kondenzací se při rostoucí relativní vlhkostí jistě zalijí všechny Knudsenovské póry (d≤10-8m) a nakonec i část pórů přechodových, asi do d=10-7m (hodnota je zhruba rovna střední volné dráze molekuly vody).
Je nyní důležité Kelvinovu rovnici správně interpretovat. K tomu je třeba si uvědomit, že tlak (nebo molární koncentrace) sytých par není (za obvyklých atmosférických tlaků) nijak ovlivněný přítomností suchého vzduchu. V Kelvinově rovnici vystupující parciální nasycený tlak nad zakřiveným povrchem p´´ (resp. parciální nasycená koncentrace c´´ tamtéž) je vlastně v tomto případě roven parciálnímu tlaku p (resp. parciální molární koncentraci c) vodní páry v daném místě pórového systému. V důsledku této nezávislé, „vnější“ veličiny automaticky musí dojít k zalití pórů odpovídajícího poloměru. Je tomu tak proto, že při dané hodnotě c resp. p bombarduje povrch menisku větší počet molekul, než je povrch ochoten uvolnit (viz vyšší vazebná síla molekul na povrchu). Proto se tato nerovnováha projeví přírůstkem kapaliny adsorbováním molekul ze vzduchu. Pohlcování se zastaví v okamžiku, kdy může být ustavena dynamická rovnováha mezi počtem pohlcených molekul (dáno kinetikou plynu) a počtem vypařujících se molekul (dáno kinetikou Maxwellovského odpařování kapaliny). Lze tedy chápat pro tyto účely parciální tlak vodní páry resp. její molární koncentraci jako hodnoty syté, k nimž se meniskus o odpovídajícím poloměru r „dotvoří“. Z rov. 11 lze potom explicitně vyjádřit závislost zalitého poloměru a tlaku nebo molární koncentrace páry ve tvaru
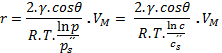
rov. 12
Poznamenejme, že sám proces kapilární kondenzace je rychlý, avšak jeho skutečná rychlost je dána tím, jak rychle je možné zásobovat meniskus kapaliny molekulami vody. K tomu slouží v dané situaci dva možné mechanismy: 3D a 2D difúze.
6. Problematika nukleace kapaliny
Pod pojmem nukleace rozumíme obecně vznik nové fáze, například růst krystalů z taveniny nebo z roztoku nebo vznik kapiček vody při kondenzaci par na částicích prachu. Místem, kde začne nová fáze vznikat, nazýváme nukleační jádra. Použijeme nyní tuto terminologii i na jevy, které vznikají v jisté analogii i u kapilárně-pórových systémů hmot.
Celý objem kapilárně-pórovitého materiálu je protkaný nesmírně hustou sítí pórů, trhlin a podobných útvarů. Tento pórový systém má z prostorového hlediska v objemu materiálu řadu míst, kde se póry významně zužují, viz obr. 9. Z pohledu transformace vodní páry na kapalinu tedy představují tato zúžení právě ta nukleační místa, kondenzační jádra, kde uvnitř pórového systému vzniká kapalina. V okamžiku vzniku kondenzačního jádra ovšem dojde k dílčímu ucpání pórového systému, takže difúze jako taková těmito místy (a tím pádem i místy které ve směru toku leží za takovou „zátkou“) nemůže probíhat. Mohli bychom tedy očekávat, že samotná 3D difúze s rostoucí vlhkostí materiálu bude klesat. Otázkou nyní je, jak se tato skutečnost reálně projeví na transportu vlhkosti materiálem. Stále přitom máme na mysli výhradně situaci, kdy jsou dvě prostředí o různé koncentraci par oddělena materiálem s kapilárně-pórovou strukturou. Neuvažujeme tedy kapilární transport vody jako kapaliny.
Nechť se tedy vodní pára pohybuje pórovým systémem, zatím za izotermních podmínek, zleva doprava. Zvolme jeden pór s úzkým hrdlem. „Řídící“ vodní pára přichází difúzními mechanismy zleva. Pára za určité hodnoty rh v hrdle kapilárně zkondenzuje na vodu a vytvoří tak v póru zátku. Meniskus se relativně rychle zalije až do poloměru r, kdy vznikne rovnováha s párou ve smyslu Kelvinovy rovnice. Otázkou nyní je, co se bude dít na opačné, „výstupní“ straně hrdla.
3D difúze
Především z důvodu ustavení hydrostatické rovnováhy se musí i na výstupní straně hrdla vytvořit meniskus o stejném poloměru, jako tomu je u na vstupní straně hrdla. Nad tímto meniskem se okamžitě vytvoří vrstvička syté vodní páry, která má stejný parciální tlak, jaký je na vstupní straně (dáno jen poloměrem menisku a teplotou). Proto zátka sama o sobě mechanismus 3D difúzního přenosu neovlivní a projeví se pouze tím, že obsah vody v materiálu poroste rychleji, než by odpovídalo samotné polymolekulární adsorpci, viz obr. 10. .
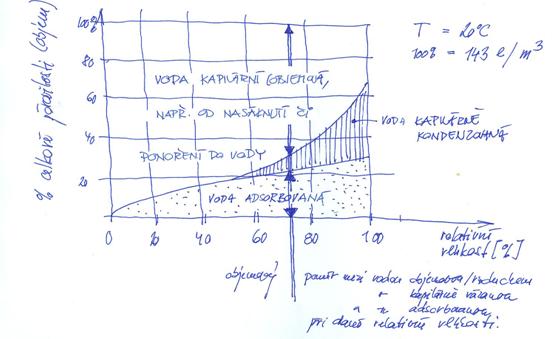
obr. 10: Lineárně rostoucí rh má za následek vlivem kapilární kondenzace rychlejší nárůst hmotnosti navázané vody, než by odpovídalo samotné polymolekulární adsorpci.
Knudsenovská difúze při vzniku kapilární kondenzace v zásadě neprobíhá (zalité póry), uplatňuje se pouze difúze v přechodové oblasti a difúze Fickovská.
2D difúze
Situace bude zjevně jiná v případě 2D difúze. Kondenzační jádra, nasycená kapalinou, poskytnou silný zdroj pro 2D difúzi. Gradient povrchové koncentrace již nebude daný rozdílem povrchových koncentrací na levém a pravém povrchu dělícího pórového materiálu. Naopak, v objemu materiálu vznikne řada dalších nukleačních míst, které poskytnou 2D difúzi zdroj molekul pro tento mechanismus. Lze proto očekávat, že v souladu s touto představou integrálně měřená veličina, totiž efektivní faktor difúzního odporu, bude s vlhkostí klesat. Přesněji: čím větší počet kondenzačních jader v materiálu vznikne, tím progresivnější bude závislost faktoru difúzního odporu na vlhkosti.
Průchod molekuly vodní páry kapilárně pórovým materiálem má – bez ohledu na mechanismus – liniový charakter. Odmyslíme-li si totiž Brownův pohyb částic a sledujeme-li elementární objem ve smyslu fyziky kontinua, tento nakonec opíše při průchodu materiálem spojitou a víceméně hladkou trajektorii. Při rostoucí relativní vlhkosti na levé straně materiálu je tedy očekávatelné, že kondenzační jádra se budou vytvářet „zleva“, tj. od míst s vysokými relativními vlhkostmi a postupně se budou množit i směrem k pravé straně. Kondenzační jádra se s rostoucím rh budou vytvářet i na liniích, kde již nějaké „zátky“ existují. Lze tedy očekávat monotónní pokles efektivního faktoru difúzního odporu s vlhkostí a to tím více, čím jemnější je kapilární systém, či spíše čím více úzkých míst (ve stereometrickém smyslu) materiál obsahuje.
7. Praktické důsledky plynoucí z rozboru
Právě provedená zjištění mají některé praktické dopady, které jednak umožňují provedené závěry experimentálně verifikovat, jednak umožňují transportní vlastnosti kapilárně pórových systémů (z pohledu molekulárního přenosu) aktivně a cíleně ovlivňovat.
Role materiálu a jeho mikrostruktury
Především se ukazuje, že při zkoumání skutečných příčin transportních procesů a jejich mechanizmů není možné odhlédnout od materiálové báze a od konkrétního charakteru pórového systému. Tato skutečnost se projevuje v následujících směrech:
1) Stereometrie systému
Daný pórový systém má určitou geometrii mikrostruktury, která a priori v geometrickém smyslu „směruje“ dráhy molekulárních (i konvektivních) látkových toků.
2) Rozměry pórového systému
Typické rozměry (např. u kapilárně pórových systémů distribuce pórů podle velikosti) zásadním způsobem rozhodují o typech a proporcích uplatnění různých přenosových mechanismů.
3) Materiálová báze
Tento faktor určuje povrchovou aktivitu materiálů. V případě biologických, makromolekulárních a dalších speciálních materiálových bází rovněž determinuje specifické přenosové mechanismy (transmise).
Obecné poznatky pro difúzní přenos v kapilárně pórových tělesech
1) Mechanismy přenosu: o převládajícím mechanismu přenosu rozhoduje pórová distribuce. V zásadě žádný běžný kapilárně pórovitý materiál stavební praxe nemá jako jednoznačně převažující mechanismus 3D difúzi, tím méně difúzi Fickovského typu. S klesajícími charakteristickými rozměry pórů stále více převažuje mechanismus 2D difúze. U hutných, jemně pórovitých materiálů typu beton, cementová malta, betonová mazanina atd. 2D difúze převažuje.
2) Faktor difúzního odporu (rozuměj efektivní, tj. měřený kalíškovými metodami) je závislý na relativní vlhkosti prostředí. Pokud chápeme faktor difúzního odporu jako jistou integrální materiálovou charakteristiku, která má v rámci zjednodušení výpočtů zohlednit všechny přenosové jevy na rozhraní dvou prostředí s různou absolutní vlhkostí vzduchu, potom takto pojímaný faktor difúzního odporu s vlhkostí klesá. Příčinou je účinek 2D difúze ve spolupráci s prostorovou sítí kondenzačních jader v místech kapilární kondenzace.
3) 2D difúze v jemněji pórovitých materiálech je nejúčinnější přenosový mechanismus. Lze ji (při daném pórovém systému) účinně čelit tím, že se podaří snížit povrchovou aktivitu materiálu. Tohoto efektu je možné docílit přidáním vhodných aditiv do materiálu, u hmot na bázi silikátových pojiv například přídavkem hydrofobů do záměsové vody.
4) 2D difúze obecně nemá shodný směr s 3D difúzí. Zatímco 3D difúze je řízena gradientem koncentrace difundujících par, u 2D difúze tomu tak není. Ve stavu termodynamické rovnováhy by byl celý vnitřní povrch materiálu pokrytý 2D vrstvičkou molekul vody (=absorbátu). 2D difúze se tedy šíří všemi směry po vnitřním povrchu, kde je tento povrch „sušší“ než v místě zdroje vodních molekul. V tom spočívá riziko povrchové hydrofobizace materiálů. Pokud bude v ploše povrchu hydrofobní povlak materiálu narušený, začne se formou 2D difúze vodní film šířit materiálem na všechny strany se stejnou rychlostí (vlhkostní „kuloplochy“).
5) 3D difúzi jde u kapilárně pórovitých těles účinně bránit nátěry povrchů jemně krystalizujícími materiály (např. Xypex). Krystaly, nukleující v pórech kapilárně pórovitého tělesa, skutečně velké póry ucpávají a snižují tak 3D difúzní toky. Neznamená to ale automaticky, že tím dochází ke snížení celkového přenosu, protože se tím aktivuje neméně výkonný mechanismus 2D difúze. Uvedené jemně krystalizující materiály jsou proto především vhodné v případech, kdy potřebujeme zabránit přenosu vody ve formě kapaliny.
8. Přenos páry v hutném betonu
V úvahách o praktickém významu jednotlivých mechanismů na celkový přenos vodní páry hraje hlavní roli jejich kvantitativní vliv. Je patrné, že díky mnohačetné propojenosti jednotlivých pórových útvarů bude výsledný difúzní tok materiálem jako jistý „vážený“ součet difúzních toků Fickovského, Knudsenovského a přechodového.
Ukažme řádový význam na rozboru přenosových mechanismů u běžného hutného betonu. Pórová distribuce byla převzata z výsledků měření, prováděných Fochstetterm /2/, tabulka 1.
Tabulka 1
1 | 2 | 3 | 4 | ||||
|
|
| Rozdělení pórů podle poloměru % (rtuťová porozimetrie) | ||||
Objemová hmotnost | pórovitost | 10-8 m | 10-8 | 10-7 | 10-6 | r>10-5 m | |
Pórobeton | 1000 | 0,595 | 2 | 62 | 21 | 5 | 10 |
Váp. písk. cihla | 1862 | 0,255 | 9 | 49 | 13 | 19 | 10 |
1950 |
https://www.izolace.cz/wp-content/uploads/2018/07/izolace-logo_340.png
0
0
Redakce IZOLACE.CZ
https://www.izolace.cz/wp-content/uploads/2018/07/izolace-logo_340.png
Redakce IZOLACE.CZ2009-06-05 00:00:002018-08-01 20:21:56Úvaha k interpretaci faktoru difúzního odporu kapilárně pórovitých materiálů
| ||||||
